Single-source Shortest Path (Weighted)

Finding shortest paths in a graph with weighted edges is algorithmically harder than in an unweighted graph because even after you find a path to a vertex T, you cannot be certain that it is a shortest path. If edge weights are always positive, then you must keep trying until you have considered every in-edge to T. If edge weights can be negative, then it’s even harder. You must consider all possible paths.

A classic application for weighted shortest path is finding the shortest travel route to get from A to B. (Think of route planning "GPS" apps.) In general, any application where you are looking for the cheapest route is a possible fit.

Specifications

The shortest path algorithm can be optimized if we know all the weights are nonnegative. If there can be negative weights, then sometimes a longer path will have a lower cumulative weight. Therefore, we have two versions of this algorithm

tg_shortest_ss_pos_wt (VERTEX source, SET<STRING> v_type, SET<STRING> e_type,
 STRING wt_attr, STRING wt_type, INT output_limit = -1, BOOL print_accum = TRUE,
 STRING result_attr = "", STRING file_path = "", BOOL display_edges = FALSE)

tg_shortest_ss_any_wt (VERTEX source, SET<STRING> v_type, SET<STRING> e_type,
 STRING wt_attr, STRING wt_type, INT output_limit = -1, BOOL print_accum = TRUE,
 STRING result_attr = "", STRING file_path = "", BOOL display_edges = FALSE)

Characteristic Value

Characteristic	Value
Result	Computes a shortest distance (INT) and shortest path (STRING) from vertex source to each other vertex.
Input Parameters	`VERTEX source`: Id of the source vertex `SET<STRING> v_type`: Names of vertex types to use `SET<STRING> e_type`: Names of edge types to use `STRING wt_attr`: Name of edge weight attribute `STRING wt_type`: Data type of edge weight attribute: "INT", "FLOAT", or "DOUBLE" `INT output_limit`: If >=0, max number of vertices to output to JSON. `BOOL print_accum`: If True, output JSON to standard output `STRING result_attr`: If not empty, store distance values (INT) to this attribute `STRING file_path`: If not empty, write output to this file. `BOOL display_edges`: If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.
Result Size	V = number of vertices
Time Complexity	O(V*E), V = number of vertices, E = number of edges
Graph Types	Directed or Undirected edges, Weighted edges

Result

Computes a shortest distance (INT) and shortest path (STRING) from vertex source to each other vertex.

Input Parameters

VERTEX source: Id of the source vertex
SET<STRING> v_type: Names of vertex types to use
SET<STRING> e_type: Names of edge types to use
STRING wt_attr: Name of edge weight attribute
STRING wt_type: Data type of edge weight attribute: "INT", "FLOAT", or "DOUBLE"
INT output_limit: If >=0, max number of vertices to output to JSON.
BOOL print_accum: If True, output JSON to standard output
STRING result_attr: If not empty, store distance values (INT) to this attribute
STRING file_path: If not empty, write output to this file.
BOOL display_edges: If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.

Result Size

V = number of vertices

Time Complexity

O(V*E), V = number of vertices, E = number of edges

Graph Types

Directed or Undirected edges, Weighted edges

The shortest_path_any_wt query is an implementation of the Bellman-Ford algorithm. If there is more than one path with the same total weight, the algorithm returns one of them.

Currently, shortest_path_pos_wt also uses Bellman-Ford. The well-known Dijsktra’s algorithm is designed for serial computation and cannot work with GSQL’s parallel processing.

Example

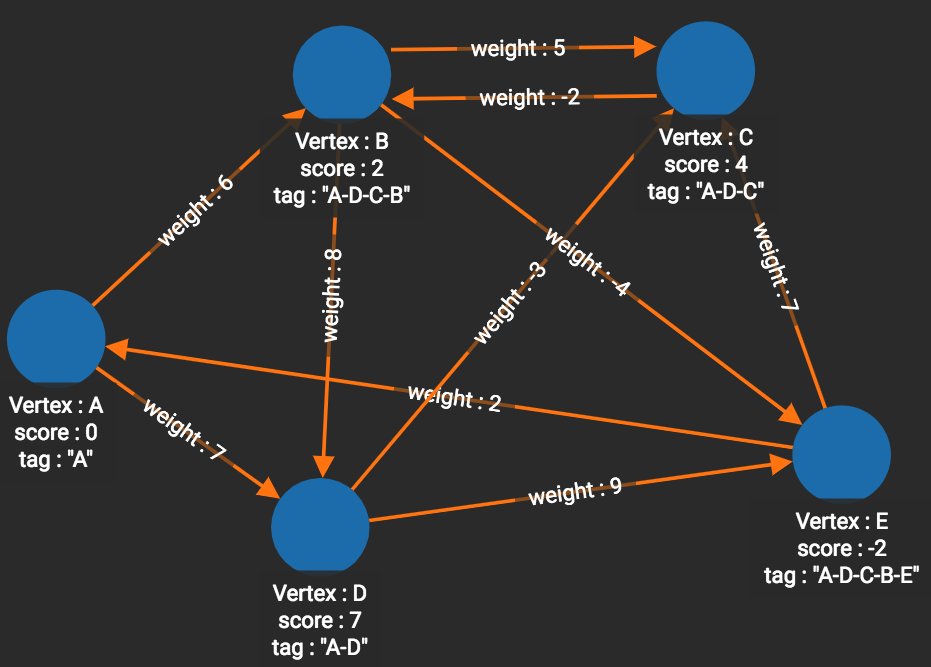
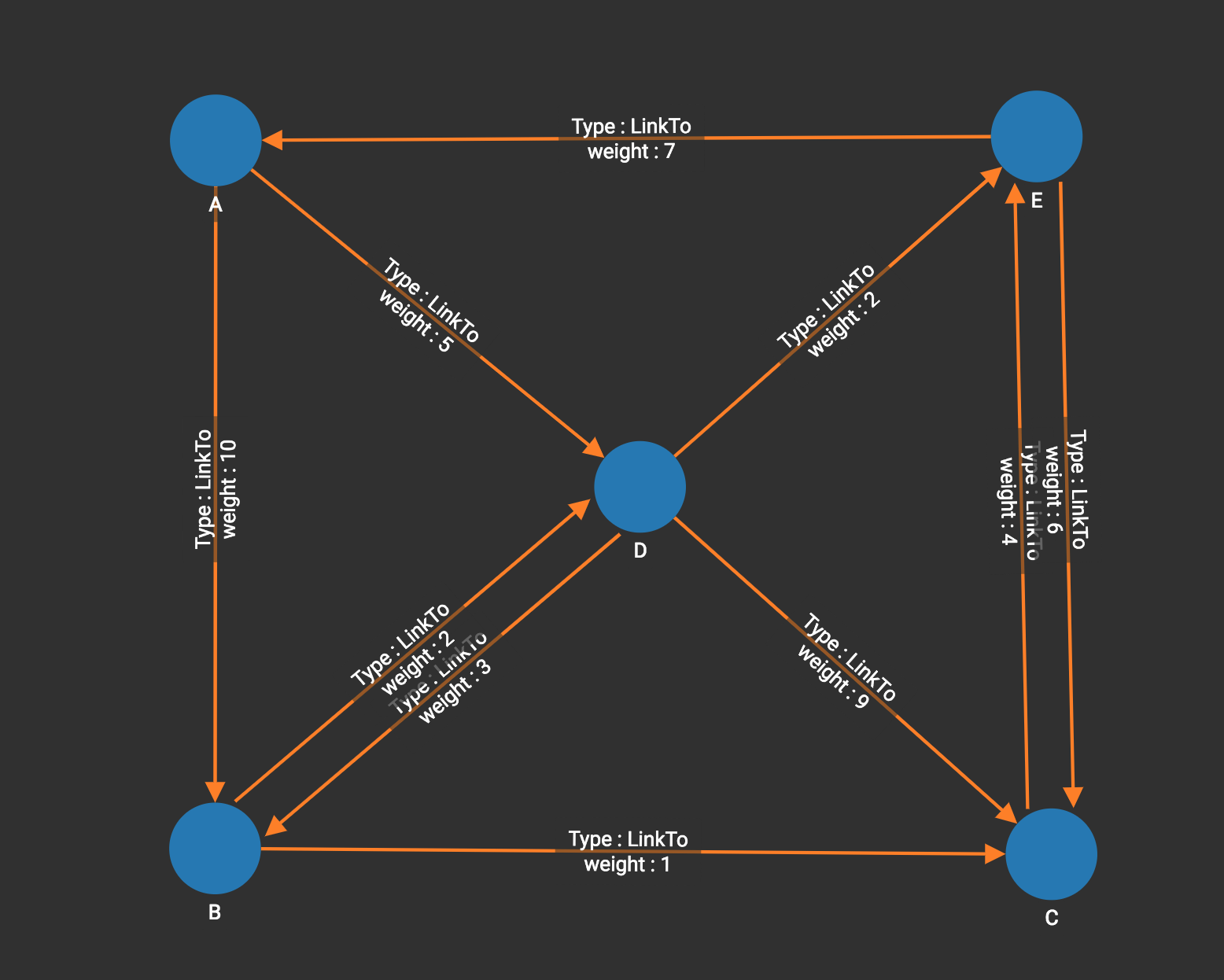
The graph below has only positive edge weights. Using vertex A as the source vertex, the algorithm discovers that the shortest weighted path from A to B is A-D-B, with distance 8. The shortest weighted path from A to C is A-D-B-C with distance 9.

Generic graph with only positive weights

[
  {
    "ResultSet": [
      {
        "v_id": "B",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 8,
          "ResultSet.@path": [
            "D",
            "B"
          ]
        }
      },
      {
        "v_id": "A",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 0,
          "ResultSet.@path": []
        }
      },
      {
        "v_id": "C",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 9,
          "ResultSet.@path": [
            "D",
            "B",
            "C"
          ]
        }
      },
      {
        "v_id": "E",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 7,
          "ResultSet.@path": [
            "D",
            "E"
          ]
        }
      },
      {
        "v_id": "D",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 5,
          "ResultSet.@path": [
            "D"
          ]
        }
      }
    ]
  }
]

The graph below has both positive and negative edge weights. Using vertex A as the source vertex, the algorithm discovers that the shortest weighted path from A to E is A-D-C-B-E, with a cumulative score of 7 - 3 - 2 - 4 = -2.

Example results on a graph with negative weights on edges