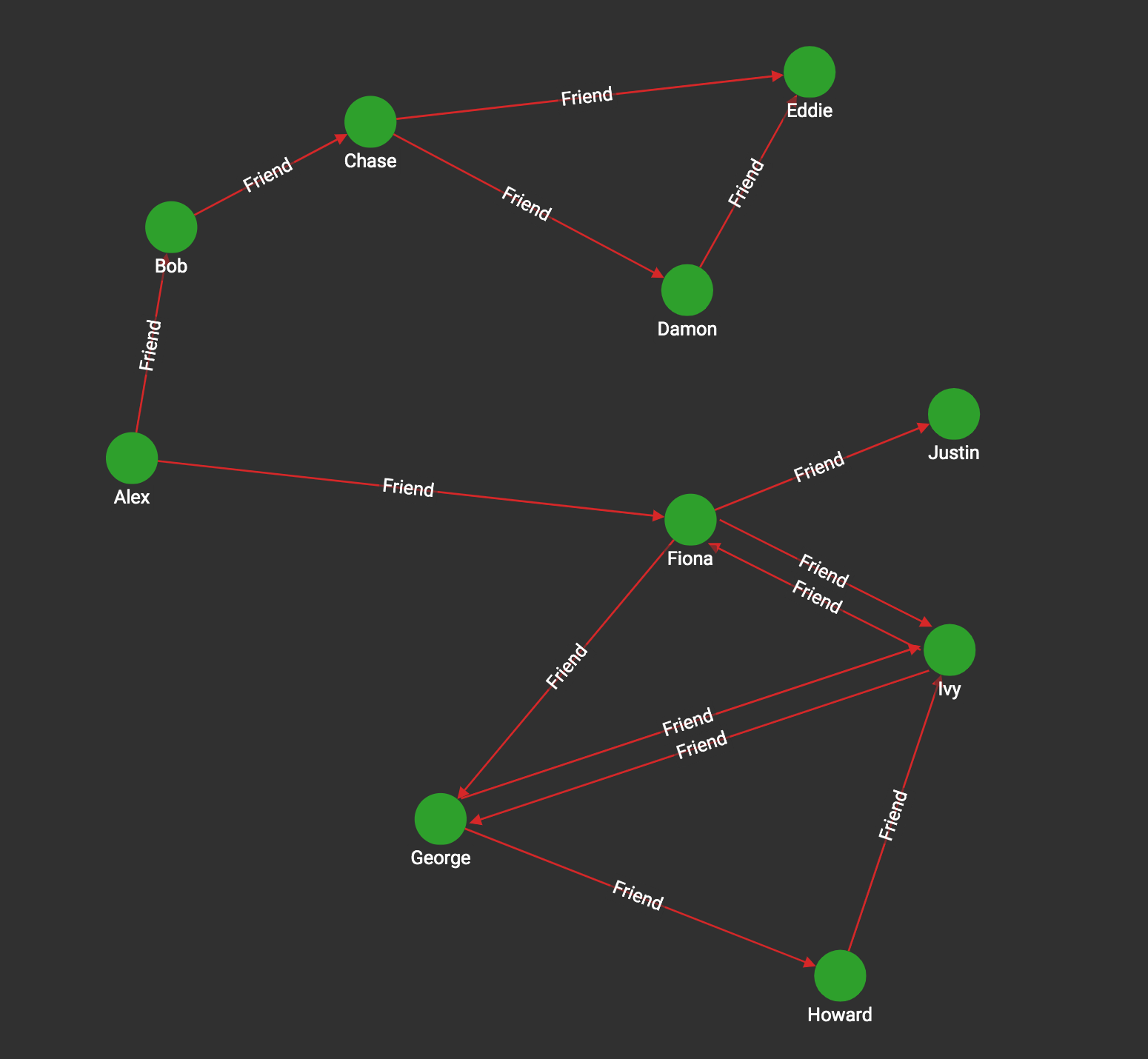
Cycle Detection
The Cycle Detection problem seeks to find all the cycles (loops) in a graph. We apply the usual restriction that the cycles must be "simple cycles", that is, they are paths that start and end at the same vertex but otherwise never visit any vertex twice.
There are two versions of the task: for directed graphs and undirected graphs. The GSQL algorithm library currently supports only directed cycle detection. The Rocha—Thatte algorithm is an efficient distributed algorithm, which detects all the cycles in a directed graph. The algorithm will self-terminate, but it is also possible to stop at k iterations, which finds all the cycles having lengths up to k edges.
The basic idea of the algorithm is to (potentially) traverse every edge in parallel, again and again, forming all possible paths. At each step, if a path forms a cycle, it records it and stops extending it. More specifically:
Initialization
For each vertex, record one path consisting of its own id. Mark the vertex as Active.
Iteration steps:
For each Active vertex v:
-
Send its list of paths to each of its out-neighbors.
-
Inspect each path P in the list of the paths received:
-
If the first id in P is also id(v), a cycle has been found:
-
Remove P from its list.
-
If id(v) is the least id of any id in P, then add P to the Cycle List. (The purpose is to count each cycle only once.)
-
-
Else, if id(v) is somewhere else in the path, then remove P from the path list (because this cycle must have been counted already).
-
Else, append id(v) to the end of each of the remaining paths in its list.
-
Specifications
tg_cycle_detection (SET<STRING> v_type, SET<STRING> e_type, INT depth,
BOOL print_accum = TRUE, STRING file_path = "")| Characteristic | Value |
|---|---|
Result |
Computes a list of vertex id lists, each of which is a cycle. The result is available in 2 forms:
|
Input Parameters |
|
Result Size |
Number of cycles * average cycle length Both of these measures are not known in advance. |
Time Complexity |
O(E *k), E = number of edges. k = min(max. cycle length, depth parameter) |
Graph Types |
Directed |